Geometry-Informed Neural Operators: Transforming 3D Fluid Dynamics Simulations
Introduction
Partial Differential Equations (PDEs) are crucial for modeling and comprehending natural events in the computer sciences, particularly in computational fluid dynamics (CFD). Even though they are precise, traditional techniques have trouble with complicated geometries and need a lot of processing power. Due to this constraint, there has been a surge in interest in using deep learning techniques, which has resulted in notable improvements in simulation efficiency.
The Challenge of Computational Fluid Dynamics
CFD simulations are pivotal for understanding and predicting fluid flow behavior in various applications, from aerodynamics to weather forecasting. Traditional numerical methods, though accurate, are computationally intensive and time-consuming, especially for large-scale simulations with complex geometries. GINO addresses these challenges head-on, providing a solution that is both faster and more adaptable than conventional methods.
The Advent of GINO
The Geometry-Informed Neural Operator (GINO), developed by NVIDIA's research team, marks a pivotal advancement in solving large-scale PDEs. By integrating signed distance function (SDF) and point-cloud data with neural operators based on graph and Fourier architectures, GINO adeptly navigates the challenges posed by irregular grids. This blend of techniques allows for efficient transformations necessary for the application of Fourier neural operators, a key feature that sets GINO apart. The architecture of GINO. The input geometries are irregular and change for each sample. These are discretized into point clouds and passed on to a GNO layer, which maps from the given geometry to a latent regular grid. The output of this GNO layer is concatenated with the SDF features and passed into an FNO model. The output from the FNO model is projected back onto the domain of the input geometry for each query point using another GNO layer. This is used to predict the target function (e.g., pressure), which is used to compute the loss that is optimized end-to-end for training.
The architecture of GINO. The input geometries are irregular and change for each sample. These are discretized into point clouds and passed on to a GNO layer, which maps from the given geometry to a latent regular grid. The output of this GNO layer is concatenated with the SDF features and passed into an FNO model. The output from the FNO model is projected back onto the domain of the input geometry for each query point using another GNO layer. This is used to predict the target function (e.g., pressure), which is used to compute the loss that is optimized end-to-end for training.
Unpacking GINO's Architecture
At its core, GINO employs a graph neural operator to manage irregular grids, facilitating their transformation into regular latent grids. This is crucial for the efficient application of Fourier neural operations. A standout aspect of GINO is its discretization-convergent nature, which ensures it adapts to various discretizations of the continuous domain, maintaining accuracy across different scales.
One of GINO's critical equations illustrates its approach to solving PDEs:
u(x)=∫Ωκ(x,y)u(y)dy
Here, u(x) represents the output function, Ω denotes the domain, and κ(x,y) is the learnable kernel function. This equation encapsulates GINO's ability to generalize neural networks, transforming them into a powerful tool for approximating complex operators between infinite-dimensional function spaces.
Empirical Validation and Performance
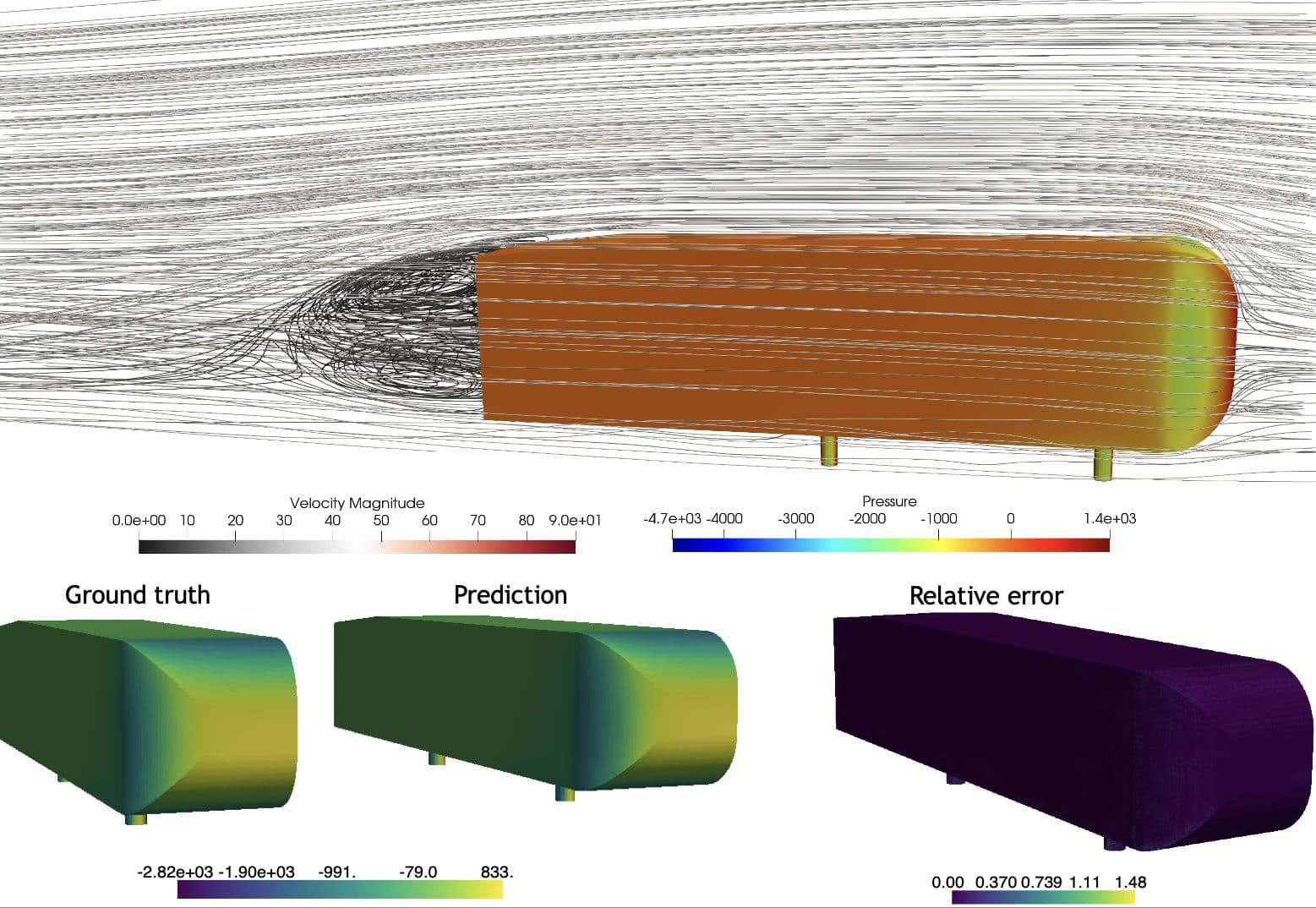
GINO's prowess was thoroughly validated against the Ahmed-Body and Shape-Net Car datasets, industry-standard benchmarks in aerodynamics. With just 500 data points, GINO showcased its ability to predict surface pressure on vehicles, a task that traditional GPU-based CFD simulators struggle with. This feat is illustrated in a side-by-side comparison of CFD simulation results and GINO's predictions, highlighting its accuracy and efficiency. Ahmed-body dataset (100k mesh points).
Ahmed-body dataset (100k mesh points).
This visual comparison underscores GINO's precision in replicating fluid dynamics phenomena, showcasing a computational speed-up of 26,000 times compared to conventional methods when calculating drag coefficients.
Future Directions
While GINO represents a significant advancement in the field of CFD, there are opportunities for further research and development. Exploring the integration of GINO with real-time data for dynamic simulation environments, extending its application to more complex fluid phenomena, and improving its adaptability to different types of geometries are areas that could yield even more groundbreaking results.
Conclusion
With its revolutionary approach to computational fluid dynamics, GINO achieves previously unheard-of levels of efficiency and accuracy by fusing deep learning with computational models. Its capacity to work with intricate geometries and adjust to various discretizations provides new avenues for investigation and development, with the potential to provide breakthroughs in the fields of science and engineering. With GINO, computational fluid dynamics appears to have a brighter future than before, signaling the start of a period of fast innovation and discovery.
Reference:
Zongyi Li, Nikola Borislavov Kovachki, Chris Choy, Boyi Li, Jean Kossaifi, Shourya Prakash Otta, Mohammad Amin Nabian, Maximilian Stadler, Christian Hundt, Kamyar Azizzadenesheli, Anima Anandkumar. "Geometry-Informed Neural Operator for Large-Scale 3D PDEs."